جلسه بیست و دوم آموزش ریاضی نهم ( حجم و مساحت کره)
درس این جلسه از دو بخش تشکیل شده است. در قسمت اول درس حجم و مساحت کره را بررسی کرده و تمرینهای مربوط به آن را حل میکنیم.
در قسمت دوم پس از معرفی هرم و مخروط ، روش به دست آوردن حجم هرم و مخروط را آموزش داده و تمرینهای کتاب را حل میکنیم.
در ادامه ابتدا مختصری از مطالب گفته شده در این جلسه را میبینید ، سپس لینک دانلود جزوه و در انتها ویدیوهای آموزشی مربوط به این جلسه
بخشهایی از درس :
حجم و مساحت کره:
در این قسمت دو تا مطلب مهم باید یاد بگیریم، اولین مطلب اینه:

توجه کنید که ما برای به دست آوردن حجم کره، فقط و فقط نیاز داریم که شعاع کره رو داشته باشیم. پس هر مساله ای که برای محاسبه حجم کره بهمون دادن ، ما از اطلاعاتش برای به دست آوردن شعاع استفاده میکنیم. پس نکته مهم برای ما پیدا کردن شعاع کره هست، چون بعد از به دست آوردن شعاع، به راحتی میتونیم حجم رو پیدا کنیم.
مثال:

الف ) گفتیم هر مساله ای که برای محاسبه حجم کره به ما داده بودن، اول به دنبال شعاع کره میگردیم. حالا از این نکته که کره در استوانه محاط شده میخوایم استفاده کنیم و شعاع کره رو به دست بیاریم.
وقتی کره در استوانه محاط میشه، چه شکلی میشه؟
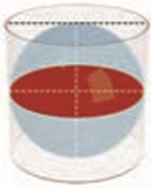
به شکل دقت کنید، چه ارتباطی بین شعاع کره و شعاع قاعده استوانه وجود داره؟
قطر قاعده استوانه = قطر کره ، بنابراین:
شعاع قاعده استوانه = شعاع کره
پس ما اگه شعاع قاعده استوانه رو داشته باشیم در واقع شعاع کره رو هم به دست آوردیم. صورت سوال به ما گفته قطر قاعده برابر 10 هست ، بنابراین:
5 = 2 ÷ 10 = شعاع قاعده
پس شعاع کره هم 5 = r هست، با استفاده از فرمول محاسبه حجم کره داریم:
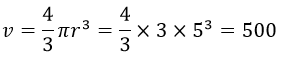
ب) قبلا یاد گرفتیم که حجم استوانه برابره با : مساحت قاعده × ارتفاع . بنابراین:
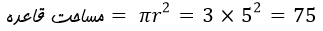
صورت سوال ارتفاع استوانه رو هم به ما داده و برابر 10 هست، بنابراین:
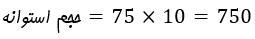
پ) حجم فضای بین کره و استوانه برابر تفاضل حجم این دو تا هست یعنی:
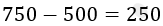
هرم و مخروط
در این قسمت از درس با “هرم” و “مخروط” آشنا میشیم.
هرم یه حجم هندسیه که کف اون چند ضلعیه و هر وجه کناریش یه مثلث
هر کدوم از شکلهای زیر یک هرم هستن:
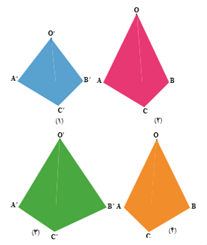
هرم دو تا عدد داره که ما توی محاسبات بهش احتیاج داریم، یکی مساحت قاعده هرم که اون رو با s نشون میدیم و یکی هم ارتفاع هرم که با h نشون میدیم.
حجم هر هرم از رابطه زیر به دست میاد:

مساحت قاعده هرم چطوری به دست میاد؟
بستگی داره به اینکه قاعده هرم چه شکلی داشته باشه. هر شکلی که داشت با توجه به رابطه مربوطه، مساحتش رو به دست میاریم.
یه شکل هندسی دیگه وجود داره که خیلی شبیه به هرمه، چه شکلی؟ مخروط
تفاوت مخروط با هرم اینه که قاعده مخروط حتما باید دایره باشه ولی قاعده هرم میتونه هر چند ضلعی که میخواد باشه.
حجم هرم و مخروط شبیه هم حساب میشه، یعنی حجم مخروط هم برابر 1/3Sh هست، ولی چون قاعده مخروط دایرهس، میتونیم به جای s مستقیما رابطه مربوط به مساحت دایره رو بنویسیم. بنابراین :
حجم مخروط با شعاع قاعده r برابر است با :
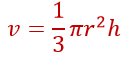
در ادامه تمرینهای صفحه 139 رو با هم حل میکنیم.
فایل کامل این جلسه را میتوانید از طریق لینک زیر دانلود کنید:
دانلود فایل کامل جلسه بیست و دوم آموزش ریاضی نهم
ویدیوی مربوط به حجم و مساحت کره :
ویدیوی مربوط به حجم هرم و مخروط :

دیدگاهتان را بنویسید