جلسه پنجم آموزش ریاضی هشتم ( تجزیه اعداد )
درس این جلسه به تجزیه اعداد و محاسبه ب م م بین دو عدد اختصاص دارد.
در ابتدای این جلسه مطالبی را از سالهای گذشته یادآوری میکنیم. این مطالب عبارتند از:
- شمارندههای اعداد
- اعداد اول
در قسمت بعد اعداد مرکب را تعریف میکنیم. سپس روش تجزیه اعداد مرکب به شمارندههای اول را آموزش میدهیم.
در قسمت پایانی درس روش به دست آوردن ب م م بین دو عدد را بررسی میکنیم.
با حل تمرین اول و پنجم صفحه 33 ، درس را به پایان میرسانیم.
در ادامه ابتدا مختصری از مطالب گفته شده در این جلسه را میبینید ، سپس لینک دانلود جزوه و در انتها ویدیوهای آموزشی مربوط به این جلسه
بخشهایی از درس:
تجزیه اعداد :
فرض کنید میخوایم عدد 60 رو به شمارنده های اول تجزیه کنیم:
اولین کاری که میکنیم اینه که دو عدد پیدا کنیم که حاصلضربشون بشه 60 .
ممکنه عددهای مختلفی پیدا بشه که ضربشون 60 باشه ولی مهم نیست که کدوم رو انتخاب کنید چون در نهایت نتیجه ها با هم برابر میشه ، مثلا میگیم :
30 × 2 = 60
عدد 60 رو مینویسیم، دو تا شاخه بهش وصل میکنیم و این دو تا عدد رو پایین شاخه ها مینویسیم، به این صورت:
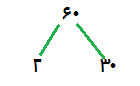
حالا باید همین کار رو واسه این دو تا عدد انجام بدیم.
دنبال دو تا عدد میگردیم که ضربشون 2 بشه، چه عددایی داریم؟
فقط این حالت وجود داره:
1 × 2 = 2
وقتی به این نقطه میرسیم دیگه این شاخه رو ادامه نمیدیم، چون به یه عدد اول رسیدیم.
“وقتی به عدد اول رسیدیم دیگه شاخه رو ادامه نمیدیم“
پس میریم سراغ عدد بعدی، یعنی 30 . دو تا عدد پیدا میکنیم که ضربشون بشه 30.
مثلا میگیم: 10 × 3 = 30
دو تا شاخه به 30 وصل میکنیم و این دو تا عدد رو پایین شاخه ها مینویسیم، به صورت زیر:
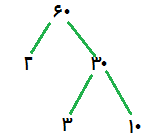
الان دو تا عدد داریم ، یکی 3 و یکی 10 .
میدونیم که 3 یک عدد اوله و دیگه نمیتونیم ادامهش بدیم ، یعنی دیگه تجزیه نمیشه.
عدد 10 چی؟ آیا میتونیم دو تا عدد پیدا کنیم که ضربشون 10 بشه؟ بله
5 × 2 = 10
اینا رو هم با دو تا شاخه به 10 وصل میکنیم، ببینید:
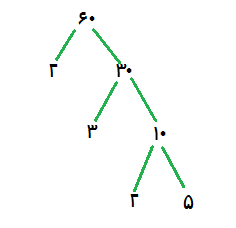
آیا 2 رو میتونیم تجزیه کنیم؟ نه، چون عدد اوله
آیا 5 رو میتونیم تجزیه کنیم؟ نه، چون عدد اوله
پس ما دیگه نمیتونیم درختمون رو ادامه بدیم.
در گام آخر، میایم دور اعدادی که دیگه قابل تجزیه نبودن خط میکشیم. به اینها برگ درخت میگن، یعنی دیگه هیچ شاخه ای در ادامهشون نیومده:
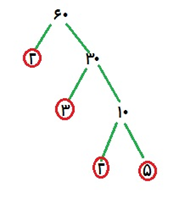
بنابراین تجزیه 60 به اعداد اول به صورت زیر میشه:
5 × 2 × 3 × 2 = 60
روش به دست آوردن ب م م دو عدد :
مثلا فرض کنید میخوایم ب م م دو عدد 18 و 30 رو بنویسیم، اول تجزیه شده این دو تا عدد رو مینویسیم (از درخت تجزیه استفاده میکنیم):
3 × 3 × 2 = 18
5 × 3 × 2 = 30
حالا دنبال اعداد مشترک بین تجزیه شده این دو عدد میگردیم.
بالا 2 داریم پایین هم 2 داریم، پس فعلا 2 رو جلوی ب م م مینویسیم:
… × 2 = ب م م
این سه تا نقطه که جلوی × گذاشتیم، به این معنیه که هنوز کارمون تموم نشده.
برای اینکه در پیدا کردن اعداد مشترک دچار اشتباه نشیم ، هر عددی مشترکی رو که پیدا کردیم و جلوی ب م م نوشتیم، در بالا و پایین خطش میزنیم، اینجا 2 رو نوشتیم پس هم در 30 و هم در 18 خطش میزنیم:
3 × 3 × 2 = 18
5 × 3 × 2 = 30
آیا باز هم عدد مشترک داریم؟ بله 3 . پس 3 رو جلوی ب م م مینویسیم و در بالا و پایین اونو خط میزنیم:
… × 3 × 2 = ب م م
3 × 3 × 2 = 18
5 × 3 × 2 = 30
آیا بین اعداد باقیمانده، باز عدد مشترک داریم؟ نه. پس اعدادی که جلوی ب م م نوشتیم رو در هم ضرب میکنیم تا جواب نهایی به دست بیاد:
6 = 3 × 2 = ب م م
بنابراین بزرگترین مقسوم علیه مشترک (ب م م) دو عدد 18 و 30 برابر 6 هست.
فایل کامل این جلسه را میتوانید از طریق لینک زیر دانلود کنید:
دانلود فایل کامل جلسه پنجم ریاضی هشتم
ویدیوی مربوط به تجزیه و ب م م (قسمت اول) :
ویدیوی مربوط به تجزیه و ب م م (قسمت دوم) :

عالی بود مرسی
خیلی عالی
خوب بود
گوود عالی